POLA DAN SUKU-SUKU BARISAN BILANGAN

B.      POLA DAN SUKU-SUKU BARISAN BILANGAN

Dalam kehidupan sehari-hari, sebagian besar masalah matematika berupa bilangan-bilangan. Bilangan tersebut ada yang diterapkan langsung dalam perhitungan, tetapi ada pula bilangan membentuk suatu aturan tertentu. Pernahkah kamu memperhatikan seorang pedagang buah jeruk menyusun dagangannya atau susunan kaleng susu yang ada di minimarket ataupun supermarket? Sengaja maupun tidak sebenarnya kita semua telah menerapkan keunikan dari suatu barisan bilangan. Pada subbab ini, kita akan belajar tentang barisan bilangan meliputi suku-suku bilangan, pola barisan, dan menemukan rumus suku ke-n dari suatu barisan bilangan.

1.      Pengertian Barisan Bilangan

Perhatikan pola bilangan-bilangan berikut.

a.       1, 3, 5, 7

b.       2, 4, 6, 8, 10

c.       3, 6, 9, 12, 15, …

Jika kalian perhatikan, bilangan-bilangan pada a, b, dan c disusun dengan pola tertentu. Bilangan-bilangan tersebut disebut barisan bilangan. Adapun setiap bilangan dalam barisan bilangan disebut suku barisan. Suku ke-n suatu barisan bilangan ditulis dengan U_n.

Pada barisan bilangan: 1, 3, 5, 7 diperoleh:

Suku ke-1 = U₁ = 1

Suku ke-2 = U₂ = 3

Suku ke-3 = U₃ = 5

Suku ke-4 = U₄ = 7

Jadi, barisan bilangan 1, 3, 5, 7 memiliki 4 suku

2.      Beberapa Contoh Aturan Barisan Bilangan

a.       Barisan dengan aturan ditambah

1)    



        Barisan bertingkat 1  

       

Barisan bilangan 1, 3, 5, 7, … merupakan barisan bertingkat satu.

2)               

Barisan bertingkat 2

Barisan bilangan  0, 1, 3, 6, … merupakan barisan bertingkat  dua.

3)    











        

Barisan bertingkat 3

Barisan bilangan  0, 1, 3, 8, 18, 35, … merupakan barisan bertingkat  tiga.

b.                 

Barisan dengan Aturan Dikali

     

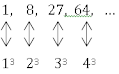
c.       Barisan dengan Aturan Dipangkatkan

         

                       

     

d.       Barisan Fibonacci

1, 1, 2, 3, 5, 8, …

Aturannya: mulai suku ketiga, setiap suku diperoleh dengan menjumlahkan dua suku sebelumnya.

3.      Menemukan Rumus Suku Ke-n (U_n)

Prinsip dasar menentukan rumus suku ke-n adalah mencari kaitan antara bilangan satu dengan suku kesatu, bilangan  dua dengan suku kedua, bilangan tiga dengan suku ketiga, dan seterusnya. Oleh karena itu, untuk bilangan n dapat dikaitkan dengan suatu bentuk aljabar dalam variabel n.

Contoh:

Barisan bilangan 2, 4, 8, 16, …

U₁ = 2      = 2¹

U₂ = 4      = 2²

U₃ = 8      = 2³

U₄ = 16    = 2⁴, dan seterusnya

Diperoleh rumus suku ke-n adalah U_n = 2ⁿ